Timed event system
The General System has been described in [Zeigler76] and [ZPK00] with the stand points to define (1) the time base, (2) the admissible input segments, (3) the system states, (4) the state trajectory with an admissible input segment, (5) the output for a given state.
A Timed Event System defining the state trajectory associated with the current and event segments is a sub-class of the class of General System. Since the behaviors of DEVS can be described by Timed Event System, DEVS is a sub-class or a equivalent class of Timed Event System.
Contents |
Timed Event Systems
A timed event system is a structure
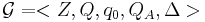
where
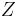 is the set of events;
is the set of events;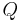 is the set of states;
is the set of states;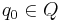 is the initial state;
is the initial state;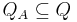 is the set of acceptance states;
is the set of acceptance states;![\Delta: Q \times \Omega_{Z,[t_l,t_u]} \rightarrow
Q](/2012-wikipedia_en_all_nopic_01_2012/I/4eb711d7b8ca5cca1fa3c1d42555558a.png) is the state trajectory function that defines how a state
is the state trajectory function that defines how a state 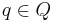 changes into
changes into 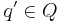 along with an event segment
along with an event segment ![\omega \in \Omega_{Z,[t_l, t_u]}](/2012-wikipedia_en_all_nopic_01_2012/I/eb8db71e91094eeb0c082d3bd74429cf.png) .
.
If 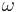 is concatenation of two unit event segments, i.e.,
is concatenation of two unit event segments, i.e., 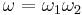 then
then
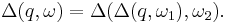
In general, if 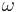 is concatenation of
is concatenation of  unit event segments, i.e.,
unit event segments, i.e., 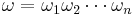 where
where 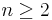 then
then
Deterministic System and Non-deterministic System
Let  and
and  be two arbitrary sets. Then function
be two arbitrary sets. Then function 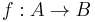 is called deterministic if for
is called deterministic if for 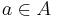 ,
, 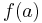 is identical any time. Otherwise,
is identical any time. Otherwise,  is called non-deterministic.
is called non-deterministic.
A Timed Event System 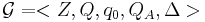 is deterministic if
is deterministic if
- selecting
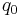 is deterministic, and
is deterministic, and  is deterministic.
is deterministic.
Otherwise, 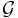 is non-deterministic.
is non-deterministic.
Behaviors and Languages of Timed Event System
Given a timed event system 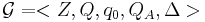 , the set of its behaviors is called its language depending on the observation time length. Let
, the set of its behaviors is called its language depending on the observation time length. Let  be the observation time length. If
be the observation time length. If 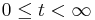 ,
,  -length observation language of
-length observation language of 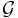 is denoted by
is denoted by 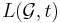 , and defined as
, and defined as
![L(\mathcal{G},t)=\{\omega \in \Omega_{Z,[0,t]}: \exists \text{ the case }
\Delta(q_0,\omega) \in Q_A\}.](/2012-wikipedia_en_all_nopic_01_2012/I/2abe3f16282b810e09b04d27e739a273.png)
Notice that the reason why we need "there exists the case" is that we allow 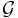 can be nondeterministic so the number of possible results
can be nondeterministic so the number of possible results 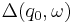 can be many. Finally, we call an event segment
can be many. Finally, we call an event segment ![\omega \in \Omega_{Z,[0,t]}](/2012-wikipedia_en_all_nopic_01_2012/I/1e6a71099cfb0190858c4938fd016a5e.png) a
a  -length behavior of
-length behavior of 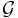 , if
, if 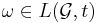 .
.
We can define behaviors with the infinite time length. Given an infinite-observation event segment ![\omega \in \underset{t \rightarrow \infty} \lim
\Omega_{Z,[0,t]}](/2012-wikipedia_en_all_nopic_01_2012/I/5daf3c6be2c95d328e1d5464dddff623.png) and a timed event system
and a timed event system 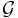 , let
, let 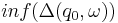 denote the set of
denote the set of 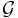 's states that are infinitely many or long visited by
's states that are infinitely many or long visited by  and
and 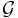 . Then infinite length observation language of
. Then infinite length observation language of 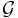 is denoted by
is denoted by 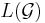 , and defined as
, and defined as
![L(\mathcal{G})= \{\omega \in \underset{t \rightarrow \infty} \lim
\Omega_{Z,[0,t]}: \exists \text{ the case }
inf(\Delta(q_0,\omega)) \subseteq Q_A \}.](/2012-wikipedia_en_all_nopic_01_2012/I/8cc123e505cfb7f54c4b37e091bfec97.png)
We call an event segment ![\omega \in \underset{t \rightarrow \infty} \lim
\Omega_{Z,[0,t]}](/2012-wikipedia_en_all_nopic_01_2012/I/5daf3c6be2c95d328e1d5464dddff623.png) an infinite-length behavior of
an infinite-length behavior of 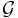 , if
, if 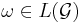 .
.
References
- [Zeigler76] Bernard Zeigler (1976). Theory of Modeling and Simulation (first ed.). Wiley Interscience, New York.
- [ZKP00] Bernard Zeigler, Tag Gon Kim, Herbert Praehofer (2000). Theory of Modeling and Simulation (second ed.). Academic Press, New York. ISBN 978-0127784557.